When I was in school, I always tought trigonometry in term of triangle. Terminologically, it is, since the word trigonometry is derived from word trigonon (triangle (tri- = three, gonia = angles/corners)) and metron (measure). So, literally, it is a measure of a triangle. However, as I re-study it a bit more to implement the principle of trigonometry, it’s more make sense to also think of it in term of a circle. We’ll discuss how to make sense some trigonometry principles in this note.

---

A Problem

Suppose a pole is 100 meters high. After several time the pole start to lean so it has \(\theta = 80^{\circ}\). When the sun is directly overhead, what’s the length of the shadow cast by this pole?

To solve this, we need to know a bit about properties of triangle.

Solution

In school, we’ve been taught to use Soh Cah Toa to find a certain side of a triangle as following

\[sin(\theta) = \frac{Opposite}{Hypotenuse}\] \[cos(\theta) = \frac{Adjacent}{Hypotenuse}\] \[tan(\theta) = \frac{Opposite}{Adjacent}\]

From the diagram, we can see that the pole forms the hypotenuse of a right triangle, the shadow is the adjacent side, and we need to find its length. Using the cosine function:

\[cos(80^{\circ}) = \frac{shadow}{100}\]

Therefore: \(shadow = 100 \times cos(80^{\circ}) = 100 \times 0.174 = 17.4 \text{ meters}\)

That might be sufficient to solve such problems algebraically. However, to grasp the concept a bit more so we could make sense another problems in engineering, we have to make sense of it based on the principles and identities in term of geometry.

Another Problem

Suppose a 2 force applied on a point.

• Force 1 have a direction toward \((0, 0)\) and have magnitude of \(5 Newton\) parallel to the x-axis.
• Force 2 have the same direction, with magnitude of \(3 N\) and \(\theta = 120^{\circ}\) relative to the Force 1. What’s the resultant of the force?

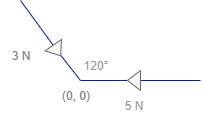
For me, by memorizing the Soh Cah Toa wouldn’t help much since we have to deal with angle beyond \(90^{\circ}\) quadrant and have to make sense the direction of the resultant.

The Meaning of \(sin(\theta)\), \(cos(\theta)\), and \(tan(\theta)\)

Suppose we have a circle with radius of 1. The value won’t matter since the properties of this geometry will scale, but we pick 1 for simplicity.

We could see \(cos(\theta)\) is actually an x-axis distance from \((0, 0)\) with the value of \(\theta\) as radians of that circle. And if we were to draw a graph from the \(cos(\theta)\) function, we would get

And for the \(sin(\theta)\) function, it is a y-axis distance from \((0, 0)\). And the graph would be

And combine both, we get a coordinate in a circle \((cos(\theta), sin(\theta))\) with \(\theta\) as a certain radian of that circle with the radius as the hypotenuse, as following

This is the key insight: any point on the unit circle can be represented as \((cos(\theta), sin(\theta))\), where \(\theta\) is the angle measured counterclockwise from the positive x-axis. This makes trigonometry much more powerful than just triangle calculations.

Values of \(\theta\) using a triangle

Using pythagoras theorem, we could actually find values of certain radians. For example, suppose if we have an equillateral triangle. Means, all angles have equal values \(\theta = 60^{\circ}\)

And divide the triangle into symetrical triangle, we would have

Let’s say the triangle have side length of 1. Because an angle in the original equillateral triangle is \(60^{\circ}\), splitted into 2, we get a right triangle with following angles:

For the \(sin(\theta)\) where \(\theta = 30^{\circ}\) it’s obvious since \(sin(30^{\circ}) = \frac{x}{1}\) and the result is \(\frac{1}{2}\) since it’s a half of original equillateral’s triangle length, that is 1.

Now if we look to another point of view, using \(sin(\theta)\) function whereas \(\theta = 60^{\circ}\) we could find using pythagoras theorem that the value of it, is \(\frac{\sqrt{3}}{2}\).

Similarly, we can construct a 45-45-90 triangle by cutting a square diagonally. This gives us the values for \(45^{\circ}\). With a hypotenuse of 1, both legs have length \(\frac{\sqrt{2}}{2}\), so:

\[sin(45^{\circ}) = cos(45^{\circ}) = \frac{\sqrt{2}}{2}\]

These fundamental angles (30°, 45°, 60°) and their trigonometric values form the foundation for understanding the unit circle.

Quadrant

A circle has a whole \(2\pi\) radians as the value. We divide this into four quadrants, each containing \(\frac{\pi}{2}\) radians or \(90^{\circ}\):

• First Quadrant (\(0\) to \(\frac{\pi}{2}\)): Both \(sin(\theta)\) and \(cos(\theta)\) are positive
• Second Quadrant (\(\frac{\pi}{2}\) to \(\pi\)): \(sin(\theta)\) is positive, \(cos(\theta)\) is negative
• Third Quadrant (\(\pi\) to \(\frac{3\pi}{2}\)): Both \(sin(\theta)\) and \(cos(\theta)\) are negative
• Fourth Quadrant (\(\frac{3\pi}{2}\) to \(2\pi\)): \(sin(\theta)\) is negative, \(cos(\theta)\) is positive

This is why the Soh Cah Toa approach breaks down for angles beyond \(90^{\circ}\) - we need to consider the signs based on which quadrant our angle falls into.

Some trigonometry Identities

Understanding trigonometry through the unit circle reveals several important identities that emerge naturally from the geometry:

Pythagorean Identity: Since any point on the unit circle satisfies \(x^2 + y^2 = 1\), and we know that \(x = cos(\theta)\) and \(y = sin(\theta)\):

\[sin^2(\theta) + cos^2(\theta) = 1\]

Reciprocal Identities: From the basic definitions:

\[tan(\theta) = \frac{sin(\theta)}{cos(\theta)}\]

\(csc(\theta) = \frac{1}{sin(\theta)}\), \(sec(\theta) = \frac{1}{cos(\theta)}\), \(cot(\theta) = \frac{1}{tan(\theta)}\)

Even and Odd Function Properties: Looking at the unit circle’s symmetry:

\(cos(-\theta) = cos(\theta)\) (cosine is even)

\(sin(-\theta) = -sin(\theta)\) (sine is odd)

Periodicity: Since the circle repeats every \(2\pi\) radians:

\[sin(\theta + 2\pi) = sin(\theta)\] \[cos(\theta + 2\pi) = cos(\theta)\]

Rework on the Problem 2

Now let’s tackle our force problem using the unit circle approach. We have:

• Force 1: 5N in the positive x-direction
• Force 2: 3N at \(120^{\circ}\) from Force 1

To find the components of Force 2:

• x-component: \(3 \times cos(120^{\circ}) = 3 \times (-\frac{1}{2}) = -1.5N\)
• y-component: \(3 \times sin(120^{\circ}) = 3 \times \frac{\sqrt{3}}{2} = 1.5\sqrt{3}N\)

The resultant force components are:

• x-component: \(5 + (-1.5) = 3.5N\)
• y-component: \(0 + 1.5\sqrt{3} = 2.598N\)

The magnitude of the resultant: \(\sqrt{3.5^2 + 2.598^2} = \sqrt{12.25 + 6.75} = \sqrt{19} = 4.36N\)

The direction: \(\theta = arctan(\frac{2.598}{3.5}) = 36.6^{\circ}\) from the positive x-axis

This approach works for any angle, not just those less than \(90^{\circ}\), because we’re thinking in terms of coordinates on the unit circle rather than just triangle sides.

Closure

By understanding trigonometry through the lens of the unit circle rather than just triangles, we gain a much more powerful tool for solving real-world problems. The circle approach naturally handles angles in all quadrants, makes the signs of trigonometric functions intuitive, and reveals the underlying geometry that connects trigonometry to vectors, waves, and many other areas of mathematics and physics.

This perspective transforms trigonometry from a collection of memorized ratios into a coherent geometric framework that extends far beyond the basic triangle problems we first encounter in school. Whether we’re dealing with forces in engineering, waves in physics, or periodic phenomena in any field, the unit circle provides the conceptual foundation we need to make sense of it all.

Cover: Photo by Dawid Małecki on Unsplash